Our infrastructure team has developed a custom automated reinforcement learning system to continuously improve our models for proving Lean theorems. A critical part of this system is our Lean execution framework, which we’ve named the REPL service. The REPL service is responsible for all interactions between our models and actual Lean proofs. This service enables our RL system to scale independently of our GPU capacity, is semantically stateless, and scales to hundreds of thousands of CPUs. All of this achieved while using preemptible instances, which are the least expensive form of computing power on the market.

In this article, we'll first provide background on Lean before describing the design constraints of the REPL service. We will then recount the story of our attempts to scale it up, including both our failures and successes. Finally, we'll outline future work and the key takeaways from this project.

Let’s get started!

Background

Lean is a powerful language designed for interactively proving theorems. Here is a partial Lean proof of the fact that if $x=2$ or $x=-2$, then $x^2=2$:

            
  theorem my_theorem (x : ℤ) (h : x = 2 ∨ x = -2) : x * x = 4 := by
    rcases h with ha | hb
    . rw [ha]
      rfl
    . have my_lemma : -2 * -2 = 4 := by sorry
      rw [hb] ; exact my_lemma
            
        

At a high level, the proof consists of tactics, such as rfl, exact, rcases, etc., each of which represents a logical “step” in the proof. At each point between tactics in a Lean proof, there is a proof state, which consists of the available variables and any already-proven facts, along with the goals, which contain what still needs to be proved. Each tactic modifies the current set of goals, producing zero or more subgoals. If no subgoals are produced, that branch of the proof is complete. Tactics may take arguments, and can be nested, as shown above.

The above proof could be represented as a tree, where the proof states are nodes (blue) and the tactics are edges (magenta):

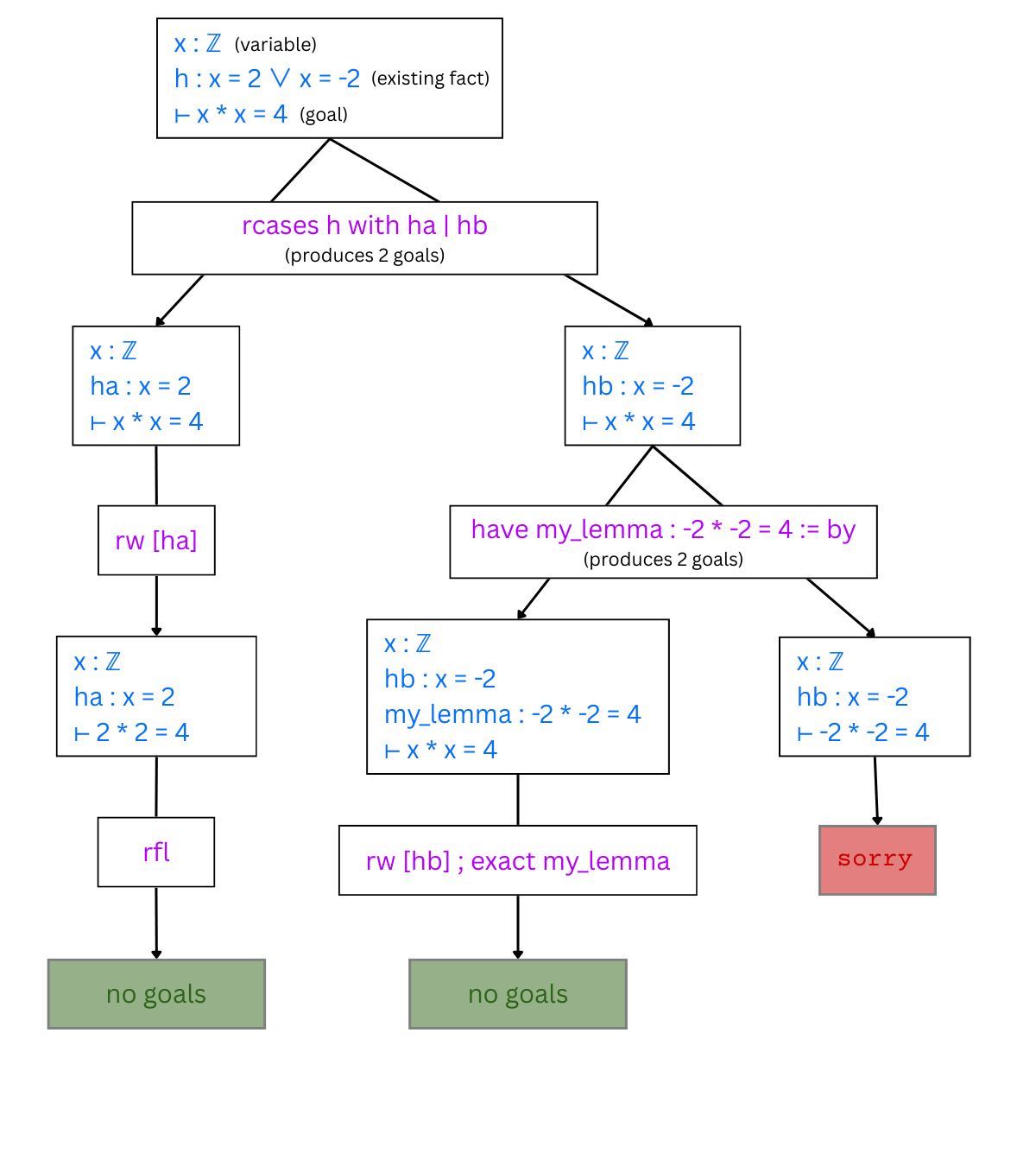
The keyword sorry means the proof is incomplete - it is our system’s job to replace sorry with a proof of the relevant fact (in this case, that $-2\times -2=4$ ). To do this, we need to explore multiple possible proof states that could arise from applying tactics at the state represented by that sorry, to find a sequence of tactics that results in no goals. We use a program called the Lean REPL for this, which (despite its name) allows us to interact with Lean proofs programmatically rather than interactively. The REPL’s basic operations are:

• Run Lean code. This operation takes a Lean file as input, and produces a set of states corresponding to each incomplete proof.
• Run tactic. This operation takes a state as input, and produces a (possibly empty) set of states as output.
• Export state. This operation returns a serialized representation of the data contained in a state, which can be loaded into another REPL process.
• Import state. This loads a state generated by the above method into the current process.

Using these operations, we can implement tree exploration by taking the original theorem statement (with one or more sorries), running it as Lean code, taking the states produced from that call, and recursively attempting to run tactics on those states. We can use the export and import state operations to “split” the tree into multiple processes, allowing us to explore multiple branches in parallel. Next, we’ll describe what is needed to do this at scale.

Requirements

The REPL service is used in many places and is critical for many of our operations, so it has strict requirements.

• It must handle Lean errors, network problems, timeouts, and other kinds of issues robustly. It isn’t acceptable for an invalid tactic to cause an unrecoverable error, for example, and the client should be able to reconnect after a timeout or other network problem and resume whatever it was doing.
• It must be able to run at a much larger scale than our GPU hardware. We need many more CPUs than our GPU-enabled machines have, and those machines have a fixed ratio of CPUs to GPUs, so simply getting more of them won’t help.
• It must run on the cheapest hardware possible. In our case, this means preemptible instances in Google Cloud Platform. This also means that it must be able to handle instance preemption gracefully.
• We must be able to autoscale this service to maintain at least 90% utilization. In the case of traffic spikes, we should be able to scale up from zero (or one) instance to the required amount and clear the queue within 10 minutes.
• The query volume could be very large, so we must be able to send many requests over the same TCP connection. Queries may take very different amounts of time, so we must also be able to send many concurrent queries per connection and receive query results out of order. Simply pipelining won’t suffice here because it would cause head-of-line blocking, which would artificially slow down fast tactics - we need a fully-asynchronous protocol.
• We must be able to share the same instance of the service between multiple client processes and GCP instances, to maximize efficiency.

With this in mind, we built a proof-of-concept that didn’t yet meet all of these requirements, but which we could use as a solid foundation.

REPL service v0

This version of the REPL service isn’t actually a service — it’s a library that runs the Lean REPL locally, and encapsulates its operations into the API described above. This is implemented in a Python class named AsyncLeanREPLProcess, which is responsible for managing the REPL process, encoding requests and decoding responses, communicating with the REPL process, and managing exported state files on the local disk. After running Lean code, AsyncLeanREPLProcess returns the unsolved goals, a list of any errors that occurred, and references to the state files on disk.

AsyncLeanREPLProcess presents an async API in order to avoid blocking the event loop, even though the underlying process is CPU-bound and can only handle a single query at a time. When multiple queries are run concurrently, we queue them up using Python’s concurrency primitives.

To run multiple REPL processes in parallel, we also created AsyncLeanREPLPool. This class presents the same interface as AsyncLeanREPLProcess, but internally delegates to a dynamically-sized pool of AsyncLeanREPLProcesses. This diagram summarizes the objects’ relationships:

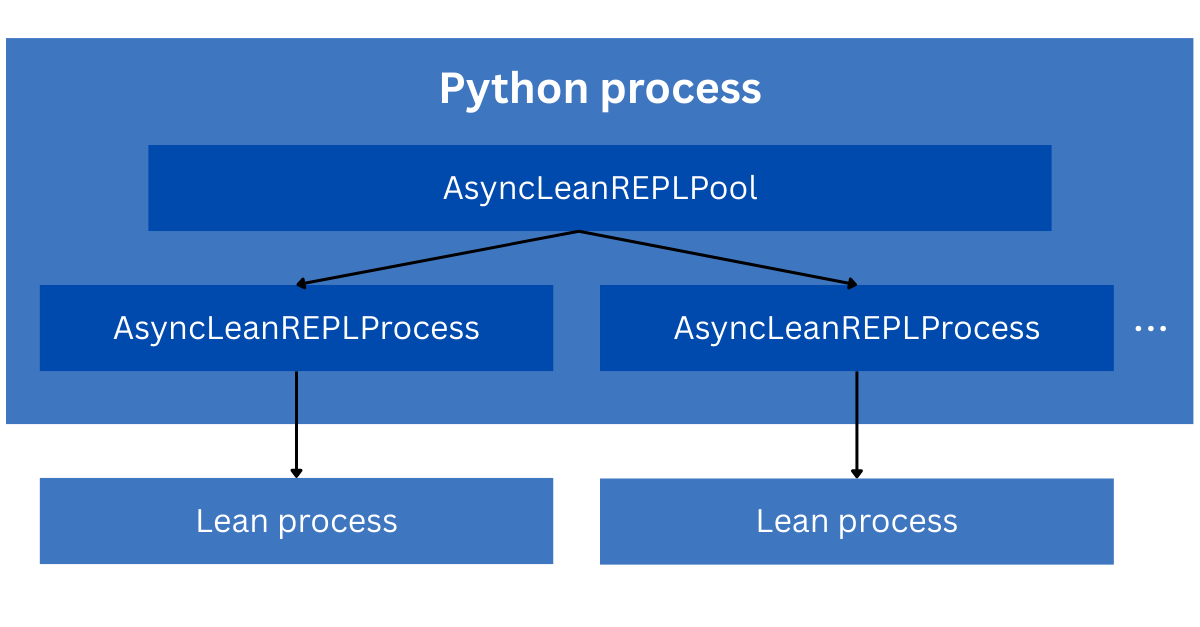
This allows a single Python process to efficiently use all of the available CPUs on the local machine to run Lean code, but still doesn’t allow us to scale beyond the limits of one machine.

To do so, we have to make this a real service.

REPL service v1: GKE, FastAPI, and WebSockets

Our first attempt at building this service was fairly simple. We set up a Google Kubernetes Engine cluster using preemptible instances and set up an application load balancer to route connections to backends. We then wrapped AsyncLeanREPLProcess in a simple FastAPI service that has a single WebSocket endpoint, over which multiple queries and responses may be sent. This architecture allows us to scale beyond one machine, but is more complex:

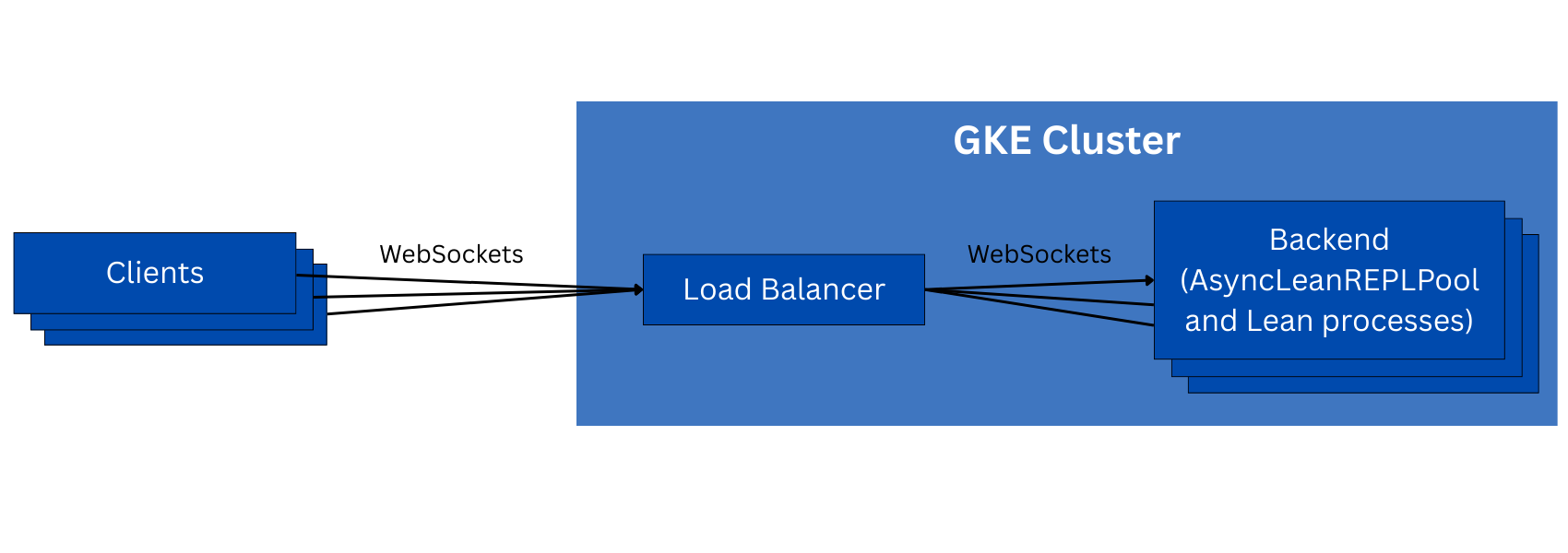
To implement out-of-order responses, we use the request ID pattern. When a method is called on the client, it creates a new future, sends its request, and waits for that future to be resolved. A background task listens for responses from the server, and resolves the correct future when each response is received. Each request and response contains a request_id field, which the client uses to look up the future to the request when a response is received. This pattern makes the client safe to use in a fully-concurrent manner, and allows the protocol to be fully asynchronous, per the requirements.

The API needed a few minor changes when scaling beyond one machine. For example, state references now have to include not only the state file name, but also the hostname of the machine that has the state data. This way, we can ensure that we don’t use the wrong state data if a query goes to a different backend and that backend happens to have a state file with the same name.

This architecture was fairly simple to build, but it ultimately didn’t work well. One major issue is that it pinned each connection to one backend, since the loadbalancer can only route entire WebSocket connections, not individual messages within a single connection. This makes it easy for the system to get into an unbalanced state, because the durations of client connections and the amount of work each one does aren't easily predictable. This makes it impossible to scale up reliably.

More importantly, this pinning behavior also causes the system to not handle disconnections well. If a client disconnects but wants to do more REPL work, it needs to reconnect and also get routed to the same backend that it was previously connected to. However, we can’t easily guarantee this using the loadbalancer since there isn’t a natural pinning key we could use — we want most connections to go to the least-loaded backend (though the loadbalancer didn’t always do this either) and only reconnections to be specially routed. The pinning behavior also means that scaling down always interrupts some connections, so this broken disconnection handling is a major problem.

Furthermore, the WebSocket connections simply weren’t reliable. We never determined a singular root cause. Sometimes it was due to node preemptions, but sometimes the connection would just get dropped even when no nodes were preempted. We suspected that this was due to the loadbalancer expecting a heartbeat that the client or server wasn’t sending in time, but the issues described above made it clear that a redesign was needed anyway, so we didn’t spend much time on this.

So, is there a way to rearchitect the service to do away with connection pinning?

REPL service v2: gRPC

Google’s application load balancers support gRPC natively, which uses HTTP/2 as a transport, and can route individual requests from one client to multiple backends. This is exactly what we want - it eliminates the pinning problems described above, but it introduces a new one: how do we make sure that the necessary state data is available on any backend that a request may be routed to? We needed to design some way to transfer state data between backends.

Fortunately, it turns out that state data compresses very well! We were able to compress state files down to about 8% of their original sizes, which made it feasible to send the state data back to the client for it to include in subsequent requests, instead of only a reference to a file on one of the backends. The service was semantically stateless after this change, so we then safely unpinned client connections from the backends.

The infrastructure for this version of the REPL service is very similar to v1:

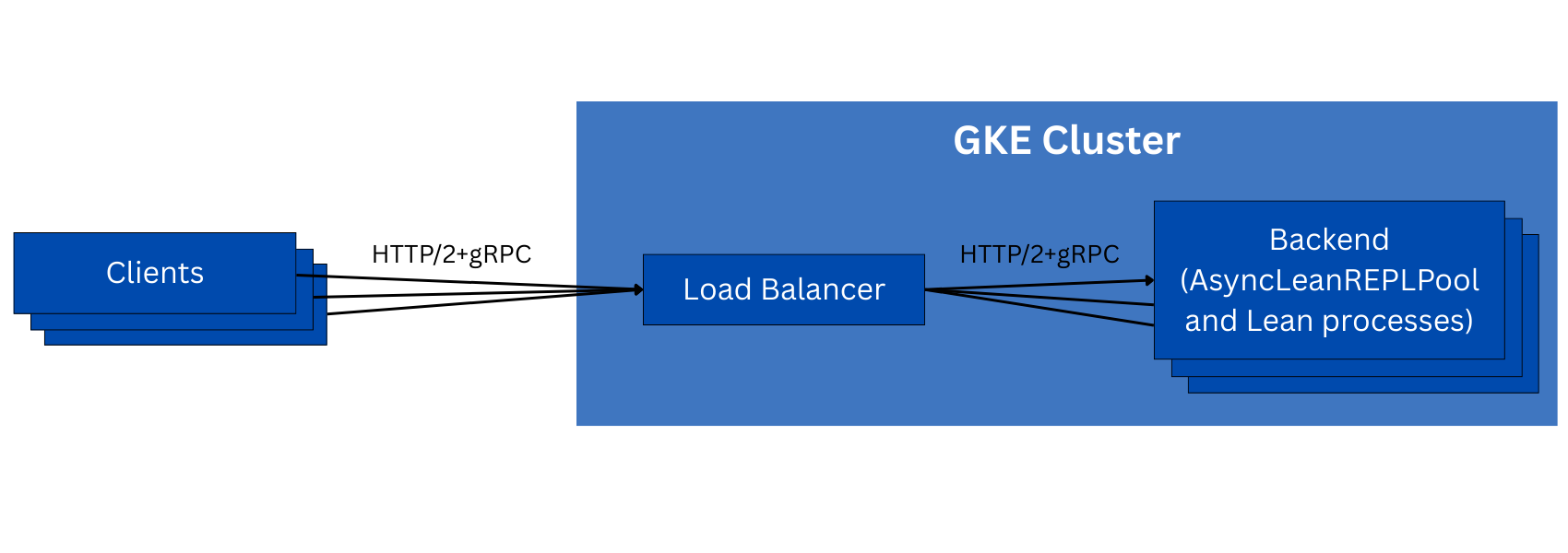
Unfortunately, this architecture didn’t work perfectly either, and we encountered many problems in building it:

• Switching to HTTP/2 is not a trivial change, even when using the official gRPC Python libraries. Encryption is not optional in HTTP/2; the load balancer requires it, the client checks the server certificate, and there’s no easy way to tell both of these entities that we’re already in a VPC and don’t need encryption. Setting up self-signed certificates works, but introduces another layer of complexity that wasn’t necessary before.
• The seemingly-random disconnection problem from v1 wasn’t fixed. This time, there’s another added layer of complexity: each HTTP/2 connection has a limit on the number of streams opened within the connection (here, a stream corresponds to a single request/response pair). This is not a limit on the number of concurrent streams, it’s a limit on the total number of streams over the lifetime of the connection! So, some of our connections that do a lot of work would be disconnected by this mechanism, and would have to reconnect manually.
• The gRPC Python client library caused problems in multiprocess environments. It creates several non-Python background threads whose state gets corrupted after a fork(), but the library automatically restarts those threads after a fork, which causes error spam at best and crashes at worst.
• There’s no global queueing on the load balancer, so there’s no way to queue requests fairly across multiple clients. Furthermore, there’s no transparency into how many requests are waiting to execute overall, how long they’ve been waiting, or how many backends would be needed to clear out the queue in a timely manner. This means we can’t implement fast scale-up, as described in the requirements.

At this point, it seemed that our problems were mostly caused by the protocol, and the complexity that comes along with it. So, we needed to switch directions again…

REPL service v3

This time, we built only what we needed, and not more. We designed a simple binary protocol; each message has a request ID, command, response count, and data. To route this protocol consistent with our requirements for fairness and autoscaling, we built a custom load balancer in C++, which is really more like a message queue. Requests from clients are immediately routed to any backend that has idle CPU capacity; if none are available, then requests go into a global queue and are forwarded as soon as any backend CPU becomes idle. The router knows how many CPUs each backend has, so it can correctly handle backends of different sizes in the same cluster. This keeps all the CPUs equally busy across the entire cluster.

Using this architecture, a single 8-core router instance can theoretically manage about 200,000 backend CPUs, but we instead run multiple smaller clusters (with one router for each) in multiple GCP regions for locality and reliability reasons.

The infrastructure looks similar to v1 and v2 at a glance:

However, there are a few significant differences from v2 that make v3 easier to work with and more reliable.

First, to simplify the router and handle backend preemption gracefully, we inverted the connection direction for the backends: they connect to the router just like normal clients, but the backends immediately send a message telling the router that they are backends rather than clients, and the router can then forward requests to them. This pattern means that the router doesn’t need to do any health checks on the backends, nor does it need to have any way to discover them - the TCP connection itself acts as the health check. (There are periodic application-layer heartbeat messages if the connection is idle.) When a backend connects to the router and sends the register message, it’s ready, and when it disconnects, it is either broken or was shut down intentionally. The router can then retry any in-progress requests that were assigned to that backend on a different backend.

Second, the router provides global request queueing, which was missing in the previous architectures. This is necessary for fairness between clients, and for autoscaling to work well. GKE’s built-in autoscaling doesn’t suffice here because there are two different behavior domains: when the queue is empty, we use GKE’s default behavior of scaling based on CPU usage, but when the queue is not empty, we expect all backend CPUs to be busy, and we want to use the queue length and processing rate instead to determine how many backends we need. The router produces timeseries metrics that include these necessary values, so we use these in a script that checks the metrics each minute and adjusts the cluster size appropriately to handle the nonempty-queue behavior domain. The algorithm is essentially:

• Measure the current request queue length (Lq), total requests completed over the past minute (Rmin), and average backend count over the past minute (Bmin)
• If Lq >= Rmin (that is, it will take at least 1 minute to clear the queue even if no more requests come in):
• Set Cm = goal time for clearing out a non-empty queue (default 5 minutes)
• Compute the processing rate (P) as Rmin / Bmin (units: requests / backend)
• Set the cluster’s minimum size to ((Rmin + (Lq / Cm)) / P) backends (reasoning: if requests come in at the same rate, there will be (Rmin + (Lq / Cm)) requests to process over each of the next Cm minutes to clear out the queue)
• Otherwise (if Lq < Rmin):
• Set the cluster’s minimum size to 1, so GKE’s CPU usage-based autoscaling will take over

This algorithm reduced our scale-up time from 1 to 100 pods from 2 hours down to 10 minutes.

This architecture solved all of the reliability problems from the previous architectures. It has per-message routing with global queueing and no connection pinning, it has fast scale-up based on the router’s metrics, the client library is implemented in pure Python with asyncio and doesn’t have background threads, and the protocol doesn’t disconnect for difficult-to-introspect reasons. When our system was working on the IMO problems this year, we didn’t have to think about this system at all, except for moving traffic around between clusters when there were CPU availability issues in some GCP regions. The process of moving traffic from hundreds of thousands CPUs in one region to hundreds of thousands in another region, required only a simple configuration change on the clients, and 10-20 minutes for autoscaling to respond.

We’re not done, however. There’s more we can do to improve this service.

REPL service v4 and beyond

We have a few ideas for making the service more efficient and functional in the future.

We could get some benefits from storing state data on disk on the router machine, instead of always sending it back to the clients. This would reduce data transfer costs when communicating with REPL clusters in a different GCP region, and would also reduce memory usage on the clients, since they would no longer need to have all the state data in memory. (For long-running processes, this can add up to a lot of memory usage!) This would make the router slower, but it’s already event-driven and multithreaded, so that’s not a major concern - we could use a separate thread pool to offload the disk I/O from the network threads. This would allow the router to implement “loose pinning” - it could preferentially send requests to backends that already have the necessary state data, if they aren’t busy, which would eliminate some network transfer time, and the time needed to decompress and import state data on the backends.

We could also use non-GKE CPU capacity as part of our REPL clusters. Some GPU machines in our infrastructure have significant amounts of CPU capacity which isn’t fully utilized; we could allow these machines to join one of the REPL clusters with some fraction of their CPUs allocated to REPL work. This would reduce our GKE costs, since we’ve already paid for these CPUs anyway, and they won’t get preempted.

Conclusion

We’ve learned a lot from this project.

There’s always a tradeoff between building something in-house vs. using an open-source or vendored product (commonly dubbed “build vs. buy”) to fill an engineering need. We find that companies usually underestimate the overhead of using an external project - it needs to be integrated into the existing system, and often doesn’t fit perfectly. In retrospect, since the in-house solution wouldn’t be worse than external systems in terms of maintenance burden and information siloing, we should have just gone for that as soon as we had the idea.

Similarly, we shouldn’t be afraid to challenge common ways of doing things. Inverting the connection direction for the backends is a good example of this - the “normal” way to write a load balancer is as a reverse proxy, but we didn’t need to implement any health checks, timeouts, or service discovery on the router in our system, which saved us a lot of time. There are good reasons why the “normal” way to do this is what it is, but those reasons didn’t apply to our use case.

Finally, it’s fun and satisfying to make systems work at large scale. At our core, we enjoy solving engineering problems in simple, elegant, and consistent ways, so scaling up a service like this is very satisfying. For a while during the IMO, we had nearly 500,000 CPUs running Lean code at the same time with 95-100% utilization, which shows that the solution we built worked.

There’s much more to do at Harmonic on this project, and on others beyond it. If this kind of work sounds interesting to you, join us!

In the wake of announcing Aristotle’s Gold Medal-level performance at this year’s International Math Olympiad (IMO) we’re releasing Yuclid and Newclid 3.0 - the systems responsible for our success on Problem 2, a plane geometry problem.

First open sourced in 2024, Newclid 2.0 was a user and developer-friendly improvement to AlphaGeometry. In collaboration with the creators of Newclid, we are releasing Newclid 3.0, a more powerful version of the previous solver, that can work on more problems and write clearer proofs than its prior iteration. We also made Newclid 3.0 easy to use; including Jupyter tutorial notebooks, full compatibility for prescribing problems with GeoGebra, sensible code, easy installation, and ample documentation to make examination and adaptation simple.

In addition to the improvements to Newclid, we developed a high-speed geometric solver engine we are also releasing today: Yuclid. Developed entirely in house, Yuclid is a proof generator that works with Newclid and can run up to 500X faster than AlphaGeometry 1. See for yourself.

Yuclid and Newclid require the support of an AI model that prescribes auxiliary points when their internal deductive reasoning is incapable of proving the goal. Aristotle was trained on synthetic data for this task, and we’re releasing the algorithm used to generate this data. In the coming weeks, we will also release a sample of synthetic JGEX problems with auxiliary constructions that can be used to train a similar model.

We’re excited to see how researchers and mathematicians will use Newclid 3.0 and Yuclid as we continue our quest for mathematical superintelligence!

Yuclid
Newclid 3.0

Today we announced live on X that our advanced formal reasoning model Aristotle achieved Gold Medal-level performance at the 2025 International Mathematical Olympiad, widely regarded as the world’s most prestigious mathematics competition. We are releasing Aristotle’s full proofs, which critically did not require human checking since they were formally verified, publicly on Github. This result places Aristotle at the forefront of advanced mathematical reasoning performance among frontier AI models.

As the world is witnessing an explosion in AI-generated content, from news articles to computer code, an unintended side-effect of this has been to turn the people using these AI tools from creators into human verifiers. In technical fields like software engineering, this means engineers spend less time coding and more time confirming the correctness of AI-generated code. We call this the verification problem, and believe it is a major bottleneck in scaling the usefulness of AI tools.

Aristotle overcomes this by design. Every solution it generates is formally verified down to foundational axioms using the Lean4 proof assistant, providing a machine-checkable guarantee of correctness. We’re starting to deploy this technology with mathematics, and we’re already working on expanding support to dependent disciplines such as physics and software engineering.

As an early look into what we expect this new verified AI technology to look like, we are launching Aristotle for iOS in Beta. When someone asks Aristotle a complex question, they not only see the solution in English but also the corresponding Lean code that verifies the correctness. Aristotle for iOS also supports photo-based solving and solving multiple questions in parallel, all with just a couple taps. Users can sign up for our waitlist at aristotle.harmonic.fun now, with the rollout already underway.

Live Announcement on X
Aristotle for iOS

Today, we’re excited to share that we’ve raised $100M in Series B funding to accelerate the development of Mathematical Superintelligence and integrate it into useful and delightful real-world applications. We’re already seeing Aristotle, our first model, aiding and enabling researchers as they drive progress in theoretical mathematics. Before too long, we believe Aristotle will be contributing to solving significant open problems, not just in mathematics but also in related fields like physics and computer science.

The $100M funding round is led by Kleiner Perkins with significant participation from Paradigm. Additional investors include Ribbit Capital alongside continued support from Sequoia Capital, Index Ventures, and Charlie Cheever.

“Harmonic has created a new foundation for verified, scalable reasoning that can be trusted in high-stakes environments. I’m deeply excited about the applications of Aristotle not just for software, but for accelerating progress across science, engineering and general intelligence,” said Ilya Fushman, partner at Kleiner Perkins and a former physicist. Fushman will join Harmonic’s Board of Directors as an observer.

If you’re interested in joining our team as we build and commercialize Mathematical Superintelligence (MSI), please check out our open roles open roles.

About a year ago, we embarked on a big mission: to create mathematical superintelligence (MSI). MSI is artificial intelligence with mathematical capabilities superior to that of humans, and we believe its development will dramatically accelerate progress in quantitative domains including science and engineering.

We're excited to announce that we've recently closed our $75 million Series A funding round led by Sequoia Capital, with significant participation by Index Ventures, and additional backing from GreatPoint Ventures, Jasper Lau's Era Funds, Blossom Capital, DST Global partners, Elefund, Nikesh Arora, and Jared Leto.

We wish to extend a big welcome to Sequoia partner Andrew Reed who will join our founders Tudor Achim and Vlad Tenev on the Board of Directors, along with Index Ventures partner Jan Hammer, who will join as an observer.

This funding provides the resources to rapidly accelerate the development of MSI. In particular, we are hiring amazing talent across research, engineering, and mathematics. If this important mission resonates with you, please see our open roles.